Three Cardinal Rules of Measurement A Deep Dive

June 25, 2023

18 minutes read

Three cardinal rules of measurement are fundamental to any accurate and reliable measurement process. They provide a framework for ensuring that our measurements are not only precise but also valid and meaningful. This exploration delves into the core principles, highlighting their historical context, various applications, and the importance of understanding accuracy, precision, and reliability.

From defining these rules to understanding their application across diverse fields, this comprehensive guide unpacks the crucial elements of measurement science. We’ll explore the vital role of units, standards, error analysis, and ethical considerations, empowering you to grasp the intricacies of this essential field.

Table of Contents

Defining the Cardinal Rules of Measurement

The foundation of any scientific endeavor, from astrophysics to zoology, rests on the ability to measure and quantify phenomena. This necessitates a framework of consistent and reliable principles, often referred to as the “cardinal rules of measurement.” These rules are not arbitrary; they stem from a deep understanding of the inherent properties of the universe and the limitations of our tools.

Speaking of precision, the three cardinal rules of measurement—accuracy, precision, and resolution—are crucial in any field, even figure skating. Alysa Liu’s stunning performance at the World Championships, taking a surprise lead in her sensational return to the sport here , highlights the importance of these rules. Perfecting those elements, like executing a triple axel with flawless form, is key to achieving top scores.

Ultimately, the core principles of measurement still apply across the board.

They’re not just guidelines; they’re the bedrock upon which reliable and comparable results are built.These rules, developed and refined over centuries, are fundamental to the very notion of objectivity in science. They provide a common language for researchers across disciplines, ensuring that measurements are understood and interpreted in a uniform manner. This allows for the comparison of results, the development of theories, and the advancement of knowledge.

Defining the Three Cardinal Rules

The three cardinal rules of measurement are principles that ensure the validity and reliability of any measurement process. These rules are not fixed but have evolved alongside the advancement of scientific instruments and methodologies.

Historical Context and Evolution, Three cardinal rules of measurement

The roots of these rules lie in the development of standardized units and measurement systems. Early civilizations, from ancient Egypt to Mesopotamia, recognized the need for consistent units of length, weight, and volume. The standardization efforts of the French during the revolution were pivotal in establishing the metric system, which continues to be the dominant system of measurement today.

Subsequent advancements in metrology, including the development of sophisticated instruments like atomic clocks and laser interferometers, have further refined the rules.

Different Interpretations and Applications Across Fields

The cardinal rules are not restricted to a single field. Their application is ubiquitous. In physics, they are used to precisely quantify the fundamental forces and properties of matter. In chemistry, they underpin the understanding of molecular interactions. In biology, they are essential for describing and analyzing biological processes.

In engineering, they provide a framework for designing and constructing reliable systems. These rules, though seemingly simple, provide a consistent language for comparison and analysis across various scientific disciplines.

Rules in a Table Format

Rule	Description	Example	Significance
Rule 1: Validity	Measurements must accurately reflect the quantity being measured. Systematic errors and biases must be minimized.	A ruler marked incorrectly will lead to invalid measurements of length.	Ensures that the measurement truly represents the quantity being measured, avoiding errors that can skew results and conclusions.
Rule 2: Reliability	Measurements must be consistent and reproducible. Random errors should be minimized through appropriate methodology and instrumentation.	Multiple measurements of the same object using the same instrument should yield similar results.	Guarantees that the measurement process is stable and reliable, allowing for the same results to be achieved if the process is repeated under identical conditions.
Rule 3: Objectivity	Measurements must be free from personal biases and subjective interpretations. Clear definitions and standardized procedures are crucial.	An observer’s preconceived notions about a measurement should not influence the reported value.	Ensures that the measurement process is not affected by personal opinions or interpretations, promoting scientific rigor and reproducibility.

Accuracy and Precision

Accuracy and precision are crucial components of any measurement process. Understanding their interplay is vital for ensuring reliable and meaningful results. These concepts are directly related to the cardinal rules of measurement, dictating the level of confidence one can place in the obtained values. Inaccurate or imprecise measurements can lead to flawed conclusions and ultimately, significant errors in applications.Accuracy refers to how close a measured value is to the true or accepted value.

Precision, on the other hand, describes the degree of agreement among repeated measurements. A highly precise measurement may not be accurate, indicating a systematic error in the measurement process. Conversely, an accurate measurement may not be precise, suggesting random errors. Ideally, a measurement should be both accurate and precise.

Relationship to Cardinal Rules

The three cardinal rules of measurement—defining the quantity to be measured, selecting appropriate tools, and recording results—all significantly impact accuracy and precision. Choosing a tool with appropriate resolution ensures precision, while meticulous adherence to measurement protocols and a well-defined procedure ensures accuracy. Understanding the limitations of the tools and methods used, and accounting for potential sources of error, is essential.

Achieving High Accuracy and Precision

Several methods can enhance both accuracy and precision in measurements. Calibration of instruments is fundamental. A calibrated instrument provides a known relationship between the measured quantity and the instrument’s output, minimizing systematic errors. Proper technique and training are equally important, reducing random errors associated with human intervention. Environmental factors can also influence measurements.

Maintaining a controlled environment during measurements can minimize the impact of these factors, contributing to both accuracy and precision.

Comparison of Methods

Calibration techniques often involve comparing the instrument’s output to a known standard. This can be achieved through direct comparison or through a traceable chain of comparisons. Proper training and adherence to standardized protocols are crucial for minimizing human error. Data analysis techniques can be employed to estimate the uncertainty associated with measurements. These methods help quantify the degree of confidence in the obtained results.

Understanding the three cardinal rules of measurement is crucial for any scientific endeavor. But, to truly innovate, you need to go beyond simply measuring; you need to create original research, which requires a specific methodology. Learning how to design and conduct such research is key ( how to create original research ). This deeper understanding of the scientific process strengthens the application of those cardinal rules and ultimately leads to more robust conclusions about the world around us.

Employing statistical analysis, such as calculating standard deviations or error margins, is a crucial step.

Measurement Tools and Their Characteristics

Measurement Tool	Typical Accuracy	Typical Precision	Application
Micrometer	±0.001 mm	High (e.g., ±0.0005 mm)	Precise measurements of small dimensions
Vernier Caliper	±0.02 mm	Medium (e.g., ±0.01 mm)	Measurements of lengths and diameters
Ruler	±1 mm	Low (e.g., ±0.5 mm)	General length measurements
Electronic balance	±0.01 g	High (e.g., ±0.001 g)	Precise mass measurements

Note: The accuracy and precision values are approximate and can vary depending on the specific instrument model and usage conditions.

Validity and Reliability

Beyond the fundamental principles of accuracy and precision, measurement systems must also possess validity and reliability to be truly useful. Validity ensures that the measurement is actually measuring what it intends to measure, while reliability guarantees that the measurement is consistent and repeatable. These concepts are intertwined and crucial for drawing meaningful conclusions from any data gathered.Understanding validity and reliability is essential for ensuring the quality and trustworthiness of measurement results.

Without them, even precise and accurate measurements may not reflect the true nature of the phenomenon being studied. This is especially important in scientific research, where the validity and reliability of measurement tools directly impact the validity of the research findings.

Validity in Measurement Systems

Validity in a measurement system assesses whether the measurement tool truly measures the intended concept. It asks whether the measurement captures the complete meaning and scope of the concept. There are different types of validity, including content validity, criterion validity, and construct validity. Content validity examines if the measurement encompasses all the relevant aspects of the concept.

Criterion validity evaluates the measurement’s relationship to other established measures of the same concept. Construct validity investigates whether the measurement aligns with the theoretical understanding of the concept.

Reliability in Measurement Systems

Reliability in a measurement system assesses the consistency and reproducibility of the measurement. A reliable measurement produces similar results when repeated under the same conditions. Different approaches exist to evaluate reliability, including test-retest reliability, inter-rater reliability, and internal consistency reliability. Test-retest reliability measures consistency over time. Inter-rater reliability evaluates consistency between different observers.

Internal consistency reliability examines the degree to which different parts of a measurement instrument yield similar results.

Examples in the Three Cardinal Rules

Accuracy: A measuring tape used to measure the length of a table must be accurate in its markings. If the tape is not accurate, the measured length will be inaccurate.
Precision: A digital scale used to measure weight must be precise in its readings. If the scale is not precise, the measured weight will fluctuate, resulting in less precise measurements.
Validity: A survey designed to measure customer satisfaction must effectively measure customer satisfaction and not something else. The questions in the survey must be valid in measuring customer satisfaction, not customer experience, or other similar concepts.
Reliability: If the same customer takes the same survey twice, the results should be consistent. If the results vary significantly, the survey lacks reliability. The survey must produce similar results over repeated measurements.

Potential Sources of Error Affecting Validity and Reliability

Instrument error: Faulty measuring instruments, like a thermometer with a malfunctioning sensor, lead to inaccurate and unreliable readings.
Observer bias: Subjectivity in the observation process can affect the accuracy and reliability of measurements. A researcher might subconsciously record data in a way that aligns with their expectations. For example, if a researcher expects a certain outcome, their observations might be biased toward confirming this expectation.
Environmental factors: Changes in temperature, humidity, or other environmental factors can affect measurements, particularly in scientific experiments. For instance, variations in temperature can alter the measurements of materials’ thermal properties.
Participant variability: Changes in participant mood, health, or other factors can affect the reliability of measurements, especially in behavioral studies.

Evaluating Validity and Reliability

Establish clear definition: Define the concept to be measured.
Develop appropriate measurement instrument: Design the tool based on the definition.
Pilot testing: Conduct preliminary trials with a small sample to assess validity and reliability.
Data analysis: Use appropriate statistical methods to analyze the data and evaluate validity and reliability indices. For example, calculate correlation coefficients to assess test-retest reliability.
Iterative improvement: Use feedback from the pilot test and data analysis to refine the measurement instrument and procedures.

Units and Standards

Measurement, at its core, relies on consistent units and standards. Without agreed-upon benchmarks, comparing results becomes problematic, and scientific progress, engineering design, and everyday life would be significantly hampered. Precise and reliable measurements are essential for ensuring accuracy and avoiding errors, which is why establishing and adhering to universal standards is paramount.Understanding the significance of consistent units and standards is crucial for anyone involved in measurement.

From scientists conducting experiments to engineers designing bridges, accurate and reproducible results depend heavily on using the same units and adhering to internationally recognized standards. This allows for effective communication and collaboration across disciplines and geographical boundaries.

Importance of Consistent Units

Consistent units are fundamental to meaningful comparisons and calculations. Imagine trying to measure the length of a room in both feet and meters simultaneously; without a conversion factor, the results would be meaningless. This highlights the critical role of standardized units in enabling efficient data interpretation and analysis. Using different units in a calculation can lead to incorrect results, which could have serious consequences in various applications.

Examples of Inconsistent Units Leading to Errors

In the construction industry, using different units for measurements can lead to serious issues. If a blueprint is drawn using feet and inches, but the workers are using centimeters, miscalculations can lead to structural problems. Similarly, in medical settings, using inconsistent units for medication dosages can result in potentially harmful consequences for patients.

Role of International Standards Organizations

International standards organizations, such as the International System of Units (SI), play a vital role in establishing and maintaining measurement standards. These organizations define internationally recognized units, ensure consistency in measurements, and facilitate communication and collaboration among scientists, engineers, and technicians globally. Their efforts are essential to fostering accurate and reliable scientific data.

Comparison of Unit Systems

Feature	Metric System	Imperial System
Basis	Based on powers of 10 (decimal system)	Based on historical units (often non-decimal)
Units for Length	Meter (m), Kilometer (km), Centimeter (cm)	Foot (ft), Yard (yd), Mile (mi)
Units for Mass	Kilogram (kg), Gram (g)	Pound (lb), Ounce (oz)
Units for Volume	Liter (L), Milliliter (mL)	Gallon (gal), Quart (qt), Pint (pt)
Advantages	Simplicity, ease of conversion, widespread adoption	Familiarity in some regions, established use in specific industries
Disadvantages	Less intuitive for some users	Complex conversions, less consistent

The table above highlights the differences between the metric and imperial systems. The metric system, based on powers of 10, is widely used in science and many parts of the world for its simplicity and ease of conversion. The imperial system, though familiar in some regions, often presents challenges due to its complex conversion factors.

Error Analysis and Mitigation

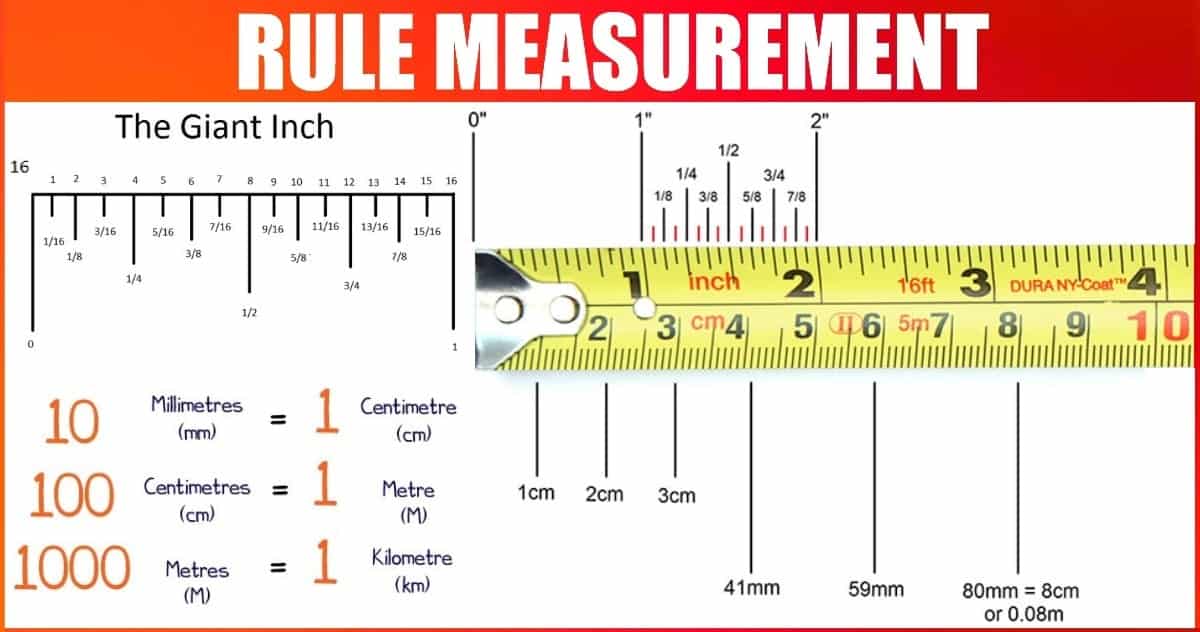
Uncertainties are inherent in any measurement process. Understanding and managing these uncertainties is crucial for obtaining reliable and meaningful results. Error analysis provides a systematic approach to identifying, quantifying, and minimizing errors in measurements, ensuring that the reported values accurately reflect the true value of the measured quantity. This process is vital in various fields, from scientific research to industrial quality control.

Common Types of Measurement Errors

Errors in measurements can arise from various sources. Systematic errors, also known as biases, consistently affect the measurement in one direction. These errors can stem from faulty instruments, incorrect calibration, or flawed experimental design. Random errors, on the other hand, are unpredictable fluctuations in the measurement results, often due to environmental factors or limitations in the measuring instrument.

These errors are typically distributed around the true value. Gross errors, often mistakes, are significant deviations from the expected values, resulting from human error, such as misreading an instrument or incorrect data entry.

Methods for Identifying and Minimizing Errors

Identifying and minimizing errors in measurements require a structured approach. Calibration of instruments is essential to ensure their accuracy and minimize systematic errors. Repeating measurements multiple times helps in identifying and averaging out random errors. Careful experimental design, encompassing the selection of appropriate measuring tools and control of environmental factors, is crucial to mitigate errors. Employing statistical methods, like calculating the standard deviation, can quantify the amount of random error in a set of measurements.

Using appropriate measurement techniques, such as using averaging or least-squares methods, can also reduce the impact of random errors. Moreover, rigorous data analysis, including error propagation calculations, ensures that uncertainties in measurements are correctly accounted for in the final results.

Examples of Error Analysis in Real-World Scenarios

Error analysis is widely applied in various fields. In engineering, precise measurements of component dimensions are crucial for ensuring structural integrity and functionality. Error analysis in manufacturing ensures the quality and consistency of products. In scientific research, experiments often involve complex measurements, necessitating meticulous error analysis to draw accurate conclusions. Consider the design of a bridge.

Precise measurements of material properties and environmental factors, combined with careful error analysis, are critical to ensuring the safety and longevity of the structure.

Step-by-Step Procedure for Error Analysis

A structured approach to error analysis can be Artikeld as follows:

Define the objective: Clearly state the purpose of the measurement and identify the relevant physical quantities to be measured.
Select appropriate instruments: Choose measuring instruments that are suitable for the measurement range and expected precision.
Calibrate the instruments: Verify the accuracy of the instruments by calibrating them against a known standard.
Conduct multiple measurements: Perform the measurement multiple times under identical conditions. Record all data meticulously.
Identify and quantify systematic errors: Analyze potential systematic errors, including calibration errors and environmental influences. Quantify the effect of these errors on the measurement results.
Identify and quantify random errors: Determine the extent of random errors by calculating the standard deviation or other relevant statistical measures. Estimate the uncertainty associated with random errors.
Propagate errors: If calculations are performed using the measured values, account for the propagation of errors through the calculations. This ensures the overall uncertainty of the final result is accurately represented.
Analyze and interpret results: Evaluate the obtained results and draw conclusions based on the calculated uncertainties.

Applications Across Disciplines

The three cardinal rules of measurement—accuracy, precision, and validity—are fundamental to all scientific endeavors. From designing bridges to diagnosing diseases, the ability to obtain reliable and meaningful measurements is crucial. This section explores how these rules are applied in diverse fields, highlighting the specific challenges and unique considerations encountered in each context.Understanding how different fields approach measurement allows us to appreciate the adaptability of the rules and the ingenuity of researchers in various disciplines.

Different methodologies may emerge for achieving the same outcome, while adhering to the cardinal rules of measurement.

Measurement in Science

Scientific measurements are vital for formulating hypotheses, testing theories, and advancing knowledge across various disciplines. Scientists strive for accuracy and precision in their measurements to ensure that their data is robust and reliable. The rigor of scientific measurement is paramount in ensuring that findings are replicable and that conclusions are drawn based on substantial evidence.

Physics: In physics, precise measurements are essential for determining fundamental constants like the speed of light or the gravitational constant. High-precision instruments, such as laser interferometers, are employed to minimize errors and enhance the accuracy of measurements. For example, experiments to verify fundamental physical laws require meticulous control over variables and careful measurement of the parameters to achieve meaningful results.
Chemistry: Chemical reactions and properties are often measured using techniques like spectroscopy and titration. The accuracy of these measurements is crucial for understanding reaction mechanisms and determining the composition of substances. For instance, in analytical chemistry, the concentration of a substance is often determined using spectrophotometry, where the absorbance of light by the solution is measured. Precise measurements of reactants and products are essential for understanding chemical reactions and formulating quantitative relationships.
Biology: Biological experiments often involve measuring various parameters like cell growth, enzyme activity, or genetic expression. Accuracy and precision are critical in these studies to ensure that observed changes are due to the experimental manipulation and not to random errors. For example, measuring the effect of a drug on cell growth requires precise quantification of cell numbers, and proper controls to account for variability.

Measurement in Engineering

Engineering relies heavily on precise measurements to design, build, and test structures and systems. Accuracy and precision in measurements are critical for ensuring that engineered products function as intended and meet safety standards. The consequences of inaccurate measurements in engineering can range from suboptimal performance to catastrophic failures.

Civil Engineering: In civil engineering, precise measurements are critical for constructing bridges, buildings, and other structures. Surveys, using instruments like Total Stations and GPS, are employed to establish precise locations and dimensions. Accurate measurements are essential for ensuring the stability and safety of structures. For example, accurate measurements of soil properties and stress levels are essential for the design of foundations to prevent structural failure.
Mechanical Engineering: Mechanical engineers use precise measurements to design machines, engines, and other mechanical components. Precision tools like calipers and micrometers are essential for ensuring that parts meet the required tolerances. For example, in the manufacturing of machine parts, dimensional accuracy is essential to ensure compatibility between components and prevent malfunctions.
Aerospace Engineering: Precise measurements are essential in aerospace engineering for navigation, guidance, and control of aircraft and spacecraft. Precise measurements of position, velocity, and acceleration are critical for flight control and safety. For example, precise measurements of the position of satellites are essential for communication and navigation systems.

Measurement in Medicine

Medical measurements are essential for diagnosing and treating patients. Accuracy and precision are crucial for making informed decisions about treatment and care. Inaccurate or imprecise measurements can lead to misdiagnosis and inappropriate treatment, potentially causing harm to patients.

Speaking of precision, the three cardinal rules of measurement – accuracy, precision, and reliability – are crucial, especially when lives are on the line. Tragically, recent wildfires in Los Angeles, with 24 dead as fire crews try to corral the blazes before winds return this week here , highlight the importance of meticulous data collection and analysis for effective response strategies.

Understanding these rules ensures accurate assessments and appropriate resource allocation, which are absolutely vital in disaster management.

Diagnosis: Medical diagnoses often rely on precise measurements of vital signs (blood pressure, heart rate, temperature) and laboratory tests (blood glucose, cholesterol). Accurate measurements are essential for detecting and monitoring diseases. For instance, precise measurements of blood pressure are essential for identifying hypertension and preventing cardiovascular complications.
Treatment: The effectiveness of medical treatments often depends on accurate measurements of drug dosages and responses. Precise measurements of medication levels in the blood are essential for adjusting dosages and preventing adverse effects. For example, accurate measurements of blood glucose levels are critical for adjusting insulin dosages in diabetic patients.
Research: Medical research relies on precise measurements to test new treatments and therapies. Precise measurements of outcomes (such as pain relief or improvement in symptoms) are essential for evaluating the efficacy of new interventions. For instance, precise measurements of tumor size before and after treatment are critical for assessing the effectiveness of cancer therapies.

Tools and Technologies

From basic rulers to sophisticated laser interferometers, the tools and technologies used in measurement have evolved dramatically. This evolution is directly tied to the pursuit of greater accuracy, precision, and reliability in our measurements. Understanding the design principles behind these tools and the advancements in technology is crucial to appreciating the power and limitations of modern measurement.

Common Measurement Tools

Various tools are essential for diverse measurement tasks. These range from simple instruments like rulers and calipers to complex devices like spectrometers and atomic clocks. The selection of a tool depends on the specific measurement being made and the desired level of accuracy. Understanding the capabilities and limitations of each instrument is critical to obtaining meaningful results.

Rulers and Calipers: These fundamental tools are used for linear measurements. Rulers provide basic length measurements, while calipers allow for more precise measurements, including internal and external dimensions. Their simplicity often necessitates careful handling to ensure accuracy. The design usually involves a rigid body with markings for measuring intervals.
Micrometers and Verniers: These instruments provide highly accurate linear measurements. Micrometers utilize a screw mechanism, allowing for very small increments, while verniers provide an enhanced scale for precise readings. These tools are often crucial in manufacturing and quality control applications, where even minute variations can affect the outcome.
Electronic Measurement Instruments: Digital multimeters, oscilloscopes, and data loggers are examples of electronic devices. These instruments utilize sensors and digital processing for measurements, often providing more flexibility and data handling capabilities compared to their analog counterparts. They frequently employ microcontrollers and sophisticated signal processing to enhance accuracy and speed.
Optical Instruments: Microscopes, telescopes, and spectrometers use light to make measurements. Microscopes reveal minute details, while telescopes expand the observable universe. Spectrometers analyze light to determine chemical composition. These instruments often leverage lenses and mirrors to focus and manipulate light for precise measurements.

Design Considerations for Adherence to Cardinal Rules

The design of measurement tools must inherently consider the three cardinal rules. For example, the design of a ruler incorporates a consistent scale and standardized units. The design of a laser interferometer incorporates high-precision components and calibration techniques to minimize error. Advanced calibration and validation techniques are also frequently incorporated to maintain the integrity of measurement results.

Advancements in Measurement Technology

Advancements in measurement technology have significantly impacted the cardinal rules. For example, the development of atomic clocks has led to unprecedented accuracy in time measurement, pushing the boundaries of precision. New technologies, such as sensors that incorporate materials with very low noise levels, improve measurement accuracy and reduce measurement error. Digital data acquisition systems have also revolutionized data processing and analysis.

Functionality of Various Measurement Instruments

Different instruments serve distinct purposes and possess unique functionalities.

Instrument	Functionality	Application
Digital Multimeter	Measures voltage, current, and resistance	Electrical circuit analysis
Oscilloscope	Displays electrical waveforms	Electronic circuit testing
Spectrometer	Measures the spectrum of light	Chemical analysis, astronomy
Atomic Clock	Provides extremely accurate time measurements	Navigation systems, scientific research

Ethical Considerations: Three Cardinal Rules Of Measurement

Measurement, at its core, is about understanding and representing the world around us. However, this process isn’t devoid of ethical implications. Inaccurate or unreliable measurements can have serious repercussions, impacting everything from public health to economic stability. Understanding these implications and fostering responsible measurement practices are paramount to ensuring the integrity of our data and the fairness of our conclusions.

Ethical Implications of Inaccurate Measurements

Inaccurate measurements can lead to a cascade of negative consequences. The consequences aren’t always immediately apparent, but the cumulative effect can be devastating. For example, faulty measurements in construction could lead to structural instability, causing injuries or fatalities. In the medical field, miscalculated dosages can have fatal outcomes, and flawed environmental assessments can delay or prevent crucial interventions.

Such errors often stem from a lack of attention to detail, inadequate calibration, or even deliberate manipulation.

Responsible Measurement Practices

Ensuring data integrity is not merely a technical concern; it’s an ethical imperative. Responsible measurement practices involve adhering to established standards, employing reliable instruments, and meticulously documenting procedures. This includes careful calibration, regular maintenance of equipment, and rigorous quality control measures. Adherence to these principles minimizes errors and builds trust in the results.

Examples of Harmful Consequences

Numerous examples highlight the potential harm caused by inaccurate measurements. One glaring example is the miscalculation of earthquake magnitudes. A miscalculation could underestimate the severity of the event, leading to insufficient emergency preparedness and response, resulting in significant loss of life and property. Similarly, flawed environmental measurements can lead to incorrect assessments of pollution levels, delaying or hindering crucial environmental protection measures.

Inaccurate product measurements can affect consumer trust and safety, especially in industries dealing with critical safety standards.

Ensuring Data Integrity in Measurement Processes

Maintaining data integrity in a measurement process requires a multi-faceted approach. A crucial element is the establishment of clear protocols and procedures, outlining the steps involved in each measurement process. Regular audits and checks on instruments are essential. Proper documentation of every step, from calibration to data entry, is paramount for traceability and verification. Furthermore, fostering a culture of accountability among those involved in the measurement process is critical.

This involves clear communication channels, training on best practices, and the development of mechanisms for reporting and addressing any discrepancies.

Outcome Summary

In conclusion, mastering the three cardinal rules of measurement is paramount for any discipline that relies on data. By understanding accuracy, precision, validity, reliability, and the crucial role of units and standards, we can ensure that our measurements are meaningful and contribute to a deeper understanding of the world around us. From scientific research to engineering design, the application of these rules is critical to progress and innovation.

We’ve explored the core principles, and hopefully, this discussion has left you with a solid foundation for understanding this critical topic.